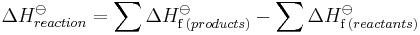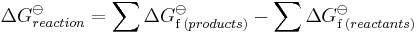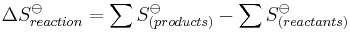Hess's law
Hess' law is a relationship in physical chemistry named for Germain Hess, a Swiss-born Russian chemist and physician.
The law states that the enthalpy change for a reaction that is carried out in a series of steps is equal to the sum of the enthalpy changes for the individual steps.
The law is an expression of the principle of conservation of energy, also expressed in the first law of thermodynamics, and that the enthalpy of a chemical process is independent of the path taken from the initial to the final state. Hess' law can be used to determine the overall energy required for a chemical reaction, when it can be divided into synthetic steps that are individually easier to characterize. This affords the compilation of standard enthalpies of formation, that may be used as a basis to design complex syntheses.
Contents |
Definition
Hess' law states that the energy change for any chemical or physical process is independent of the pathway or number of steps required to complete the process provided that the final and initial reaction conditions are the same. In other words, an energy change is path independent, only the initial and final states being of importance. This path independence is true for all state functions.
Hess' law allows the enthalpy change (ΔH) for a reaction to be calculated even when it cannot be measured directly. This is accomplished by performing basic algebraic operations based on the chemical equation of reactions using previously determined values for the enthalpies of formation.
Addition of chemical equations may lead to a net equation. If enthalpy change is known for each equation, the result will be the enthalpy change for the net equation. If the net enthalpy change is negative (ΔHnet < 0), the reaction is exothermic and is more likely to be spontaneous; positive ΔH values correspond to endothermic reactions. Entropy also plays an important role in determining spontaneity, as some reactions with a positive enthalpy change are nevertheless spontaneous.
Hess' Law states that enthalpy changes are additive. Thus the ΔH for a single reaction can be calculated from the difference between the heat of formation of the products and the heat of formation of the reactants:
where the o superscript indicates standard state values.
Use
To use Hess's law to compute enthalpy changes for reactions, two rules must be followed:
1. If a reaction is reversed, the sign of ΔH is also reversed.
2. The magnitude of ΔH is directly proportional to the quantities of reactants and products in a reaction. If the coefficients in a balanced reaction are multiplied by an integer, the value of ΔH is multiplied by the same integer.
Calculations involving Hess's law typically require that several reactions be manipulated and combined to give the reaction of interest. In doing this procedure, it may be helpful to work backward from the required reaction, using the reactant and products, and then multiply the reactions to give the correct numbers of reactant and products.
Table of data for a Hess' law calculation:
| Substance | ΔH |
|---|---|
| CH4 (g) | -75 |
| O2 (g) | 0 |
| CO2 (g) | -394 |
| H2O (l) | -286 |
Using this data, ΔHoc for the reaction below can be found:
-
- CH4 (g) + 2 O2 (g) → CO2 (g) + 2 H2O (l)
-
- ΔH
oc = [-394 + 2(-286)] - [-75 + 2(0)] = -891 kJ/mol
- ΔH
Example
Given:
- B2O3 (s) + 3 H2O (g) → 3 O2 (g) + B2H6 (g) (ΔH = 2035 kJ/mol)
- H2O (l) → H2O (g) (ΔH = 44 kJ/mol)
- H2 (g) + (1/2) O2 (g) → H2O (l) (ΔH = -286 kJ/mol)
- 2 B (s) + 3 H2 (g) → B2H6 (g) (ΔH = 36 kJ/mol)
Find the ΔHf of:
- 2 B (s) + (3/2) O2 (g) → B2O3 (s)
After the multiplication and reversing of the equations (and their enthalpy changes), the result is:
- B2H6 (g) + 3 O2 (g) → B2O3 (s) + 3 H2O (g) (ΔH = -2035 kJ/mol)
- 3 H2O (g) → 3 H2O (l) (ΔH = -132 kJ/mol)
- 3 H2O (l) → 3 H2 (g) + (3/2) O2 (g) (ΔH = 858 kJ/mol)
- 2 B (s) + 3 H2 (g) → B2H6 (g) (ΔH = 36 kJ/mol)
Adding these equations and canceling out the common terms on both sides, we get
- 2 B (s) + (3/2) O2 (g) → B2O3 (s) (ΔH = -1273 kJ/mol)
Given:
Net reaction: C(s) + ½ O2(g) + H2O(ℓ) → H2CO2(ℓ)
Reaction 1: C(s) + ½ O2(g) → CO(g) ΔH1 = -110.5 kJ
Reaction 2: CO(g) + H2O(ℓ) → H2CO2(g) ΔH2 = +33.7 kJ
Reaction 3: H2CO2(g) → H2CO2(ℓ) ΔH3 = -62.9 kJ
To apply Hess's law, sum reactions 1, 2, and 3 and cancel any species common to the products and reactants in the reaction.
1 + 2 + 3: C(s) + ½ O2(g) + CO(g) + H2O(ℓ) + H2CO2(g) → CO(g) + H2CO2(g) + H2CO2(ℓ)
Cancel: C(s) + ½ O2(g) + CO(g) + H2O(ℓ) + H2CO2(g) → CO(g) + H2CO2(g) + H2CO2(ℓ)
Net reaction: C(s) + ½ O2(g) + H2O(ℓ) → H2CO2(ℓ)
The net reaction is the sum of reactions 1, 2, and 3, and therefore the enthalpy change for the net reaction is equal to the sum of the enthalpy changes for reactions 1, 2, and 3.
ΔHrxn = ΔH1 + ΔH2 + ΔH3 = (-110.5 kJ) + 33.7 kJ + (-62.9 kJ) = -139.7 kJ
<http://s-college.cengage.com/nextbook/vining/vining_owlbook_prototype/ebook/ch5/Sect5-5-a.html />
Extension to entropy and free energy
The concepts of Hess' law can be expanded to include changes in entropy and in Gibbs free energy, which are also state functions. The Bordwell thermodynamic cycle is an example of such an extension which takes advantage of easily measured equilibriums and redox potentials to determine experimentally inaccessible Gibbs free energy values. Combining ΔGo values from Bordwell thermodynamic cycles and ΔHo values found with Hess' law can be helpful in determining entropy values which are not measured directly, and therefore must be calculated through alternative paths.
For the free energy:
For entropy, the situation is a little different. Because entropy can be measured as an absolute value, not relative to those of the elements in their reference states (as with ΔHo and ΔGo), there is no need to use the entropy of formation; one simply uses the absolute entropies for products and reactants:
See also
References
- Chakrabarty, D.K. (2001). An Introduction to Physical Chemistry. Mumbai: Alpha Science. pp. 34–37. ISBN 1-84265-059-9.
Further reading
- Leicester, Henry M. (1951). "Germain Henri Hess and the Foundations of Thermochemistry". The Journal of Chemical Education 28 (11): 581–583. Bibcode 1951JChEd..28..581L. doi:10.1021/ed028p581.